الأنظمة العددية | Système de Numération

فهاد المقال غادي نرجعو شويا ذكريات الرياضيات، لي كتعتابر جميلة بالنسبة للبعض وكابوس بالنسبة للبعض الآخر هههه. لكن ماغاديش نخدمو بكاع الرياضيات غانخدمو غير بالمضاعافات وبالأس والعمليات ديال الضرب والقسمة والجمع..

الأنظمة العددية يمكن لينا نعتابروها واحد الطريقة لتمثيل أو كتابة الأرقام برموز محددة على حسب القراءة لي بغينا نقراوها بها.. ربما يبان ليك التعريف شويا مخربق لكن الى كملتي معايا حتى للأخير غادي تفهم..

فهاد الأنظمة العددية كنلقاو بزااف ديال النظم أو كما كنسميوهم بالفرنسية les bases

غير حنى كنخدمو بربعة لي مشهورين ولي هما:

Binaire, Octal , Décimal, Hexadécimal

Binaire | النظام الثنائي :

هذا نظام كيتكون من 2 أرقام، داكشي علاش كنقولو ليه ثنائي:

والأرقام لي كيتكون منها هاد النظام هي: 1 و 0 ، وهاد الرقمين هما اللغة لي كيفهمها الحاسوب.. كيعرف فقط الواحد والصفر، كيفاش كيدير لها وداكشي لاخر غاتفهموه من بعد. Décimal | النظام العشري :

هذا نظام كيتكون من 10 أرقام، داكشي علاش كنقولو ليه:

la base 10

والأرقام لي كيتكون منها هاد النظام هي: 0 و 1 و 2 و 3 و 4 و 5 و 6 و 7 و 8 و 9 ، وهاد الأرقام هما الأرقام لي كيخدم بهم الإنسان فجميع المجالات ومنهم كنقدرو نكونو بزاف دالأرقام آخرين

Octal | النظام الثماني :

هذا نظام كيتكون من 8 الأرقام، داكشي علاش كنقولو ليه:

la base 8

والأرقام لي كيتكون منها هاد النظام هي: 0 و 1 و 2 و 3 و 4 و 5 و 6 و 7 ، وهاد لاباز ديما غاتلقاوها كتكون من 3 أرقام لي كيبداو من اليمين نحو اليسار، وغاتلقاو فكل عدد غير هاد الأرقام لي ذكرنا الفوق.. يعني مايمكنش تلقى رقم 8 فشي لابز ديال الاوكتال.. غادي تلقى من 0 حتى لـ 7 فقط….

:Hexadécimal | النظام السداس عشري

هذا نظام كيتكون من 16 رقم، داكشي علاش كنقولو ليه :

la base 16

والأرقام لي كيتكون منها هاد النظام هي: 0 و 1 و 2 و 3 و 4 و 5 و 6 و 7 و 8 و 9 و A و B و C و D و E و F ، بالنسبة للحروف:

A=10 ، B=11 ، C=12 ، D=13 ، E=14 ، F=15

السبب علاش كتبنا الحروف وماكملناش بالطريقة ديال الأرقام، لأننا الى كتبنا 15 غادي تعتابر فالحساب ديال الأنظمة العديدة على أنها جوج أرقام ولي هما 1 و 5 ، داكشي علاش ملي كيكون عندنا عدد مكون من رقمين كنكتبوه على شكل حرف. لكن في حدود الحرف F طبعا لي كيتعتابر آخر حرف فلاباز 16 , وفالهيكزاديسيمال غاتلقى ديما عدد مكون من أربعة أرقام. .

ندوزو دبا للطريقة ديال التحويل من باز لباز أخرى.. ونبداو مع الديسيمال..

باش نحولو من لاباز ديال الديسيمال لأي باز كيف ما كانت كنعتامدو على قاعدة وحدة كنطبقوها على كولشي.. وباش مانخربقكمش ما غاديش نعطيكم ديك القاعدة ديال الرياضيات. لأنني عارف بلي كلكم كتكرهو دوك القواعد وما كيدخلوش ليكم لراسكم... لذلك غانعتامد على مثال.. لأنه بالمثال يتضح المقال:

(128)₁₀= (10000000)₂

كنظن أن الفكرة وصلات.. كناخذو العدد لي عطاونا وكنبداو نقسموه على 2 هاذي بالنسبة للتحويل إلى البينير..

أجيو دبا نشوفو باز أخرى ولنأخذ لاباز أوكتال.

(128)₁₀= (200)₈

نفس القاعدة ولي هي القسمة.. مع تغيير العدد لي كنقسمو عليه.. حيت حنى خدامين دبا فالاوكتال غادي نخدمو برقم 8 .. وحيت فالمثال الأول كنا خدامين بالبينير خدمنا برقم 2 .. وإلى بغينا نخدمو فالهيكزاديسيمال اشمن رقم غانخدمو بيه؟ نخليكم نتوما لي تحولو للهيكزاديسمال باش ترسخ ليكم الفكرة أكثر.

دبا نشوفو كيفاش نحولو من أي باز للديسيمال

حتى هي عندها قاعدة كنمشيو عليها.. ناخذو أمثلة:

Binary to Decimal:

(11100100)₂= (1*2⁷)+ (1*2⁶) + (1*2⁵) + (0*2⁴) + (0*2³) + (1*2²) + (0*2¹) + (0*2⁰)

(11100100)₂= 128 + 64 + 32 + 0 + 0 + 4 + 0 + 0

(11100100)₂= (228)₁₀

الحساب واضح لكن ربما لي غير مألوف وغير مفهوم بالنسبة ليكم هو منين جبنا دوك الأس كاملين.. وكيفاش حتى درناهم ؟

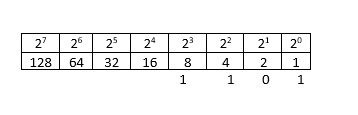
عندنا فكل بت كيكون واحد الأس.. وهذاك الأس هو لي كيحدد لينا القيمة ديالو.. كنبداوه ديما من اليمين وكيكون عندنا على هاد الشكل

هاكا كنحطوهم فورقة الوساخ أو فعقلنا.. وكنبداو نحسبوهم.. كل رقم كنضربوه فالرقم والأس المقابل ليه وكنديرو عملية الجمع كما هو متضح فالمثال أعلاه.

ناخذو مثال آخر باش توضاح الفكرة اكثر.. ونخدمو هاد المرة على الهيكزاديسيمال..

Hexadecimal to Decimal:

(AC12)₁₆= (A*16³) + (C*16²) + (1*16¹) + (2*16⁰)

(AC12)₁₆= 40960 + 3072 + 16 + 2

(AC12)₁₆= (44050)₁₀

درنا نفس الطريقة مع تغيير لاباز.. حيت دبا ولينا خدامين فالهيكزاديسيمال داكشي علاش درنا 16

نفس الشيء غانديروه حتى مع التحويل من الأوكتال للديسيمال.. غير غانبدلو لاباز هاد المرة وغانخدمو بـ 8

كمثال:

Octal to Decimal:

(270)₈= (2*8²) + (7*8¹) + (0*8⁰)

(270)₈= 2*64 + 7*8 + 0

(270)₈= 128 + 56

(270)₈= (184)₁₀

كنظن الفكرة وصلات بلاما نحتاج نشرح شنو درنا..

دبا عرفنا كيفاش نحولو من أي باز للديسيمال وعرفنا كيفاش نحولو من الديسيمال لأي باز أخرى..

بقى لينا نعرفو كيفاش نقدرو نحولو من الأوكتال للبيينير ومن الهيكزاديسيمال للبينير والعكس

اوكي, ركز معايا دبا باش مايبقاش عندك مشكل فهادشي بمرة.. نبداو بكيفاش نحولو من البينير للأوكتال

غانعتامدو على هاد الجدول لي غايعاوننا وخاصك تكون حافظو.. والى ما كنتيش من عشاق الحفاظة فهمو وغاتبقى عاقل عليه:

Binary to Octal:

2(110111001)

عندنا هاد الرقم فالبينير ومطلوب منا نحولوه للأوكتال.. إلى عقلتو فأول الدرس قلنا أن الأوكتال كيكون متكون من 3 الأرقام فكل عدد وديما بدءا من اليمين نحو اليسار.. إذن باش نحولو حنى هاد العدد غادي نشدوه ونقسموه على ثلاثة بدءا من اليمين, وغادي يولي لينا بهاد الشكل:

110 111 001

ودبا غايسهال علينا باش نحسبوه ونرجعوه أوكتال:

(110111001)₂= 671

السؤال المطروح دبا هو كيفاش درنا ليها ؟ الجواب سهل..

قسمناهم على ثلاثة وحسبنا كل ثلاثة الأرقام شحال كيساويو عن طريق داك الجدول لي ذكرنا الفوق بالاعتماد على الطريقة ديال الأس لي كنا استعملناها فالأمثلة السابقة.. يعني كل رقم شفنا اشمن أس كيقابلو..

نزيد نوضح أكثر, تعمدت ندير الأرقام بالألوان باش نعرفو كل لون شحال كيساوي لينا..

نبداو باللون الأحمر 001

رقم 1 كيقابلو 2⁰

رقم 0 كيقابلو 2¹

رقم 0 كيقابلو 2²

الأصفار بجوجهم ماغاديين يعطيونا والو حيت ملي غانضربوهم فالعدد والأس لي مقابلهم غايعطيونا 0

والواحد لي بقى لينا إلى ضربناه فـ 2⁰غايعطينا 1

ندوزو للون الأزرق 111

رقم 1 كيقابلو 2⁰

رقم 1 كيقابلو 2¹

رقم 1 كيقابلو 2²

1*2⁰= 1

1*2¹ = 2

1*2² = 4

1+2+4 = 7

وهاذي هي النتيجة لي خرجات لينا نيت..

نفس الشيء درناه مع اللون الأخضر 110

رقم 0 كيقابلو 2⁰

رقم 1 كيقابلو 2¹

رقم 1 كيقابلو 2²

1*2⁰= 0

1*2¹ = 2

1*2² = 4

0+2+4 = 6

وهاذي هي الطريقة بكل بساطة.. خاص غير شويا ديال الممارسة وغاتعلم هادشي بزربا.

نشوفو دبا من الأوكتال للبينير كيفاش غادي نحولو:

Octal to Binary:

(653)₈

غادي ناخذو هاد ثلاثة الأرقام ونخليو كل رقم بوحدو.. ونشوفو شحال كيساوي عن طريق الجدول لي ذكرنا الفوق..

نبداو برقم 3 فالجدول كتساوي لينا: 1 و 2 لأن 1+2 = 3 طبعا إذن كنجيو كنعوضو دوك الأرقام بالكتابة ديال البينير لأننا حنى باغيين نحولو للبينير طبعا.. والبينير هو رقم 0 و 1 إذن غانكتب: 11 لكن عندي مشكل دبا ولي هو أنا كنعرف أن الاوكتال كيكون متكون من ثلاثة الأرقام ماشي جوج, إذن غانزيد واحد الصفر وغاتولي على هاد الشكل: 011 ودبا الكتابة صحيحة.

ندوزو دبا لرقم 5 ولي فالجدول كيساوي لينا: 1 و 4 لأن 1+4= 5 , ولكن الى شفت فالجدول غانلقى ان بين 1 و 4 كاين رقم 2 وانا ما عندي ماندير بديك 2 إذن غانجي ونبدا نعوض بهاد الشكل: 101 عوضت 1 و 4 برقم 11 وبقات ليا ديك 2 لي بيناتهم عوضتها ب 0 وهاكا حصلت على الأوكتال ديالي.

رقم 6 فالجدول كيساوي لينا: 2+4 إذن كنبداو نعوضو مباشرة 11 غايبقى خاصني رقم باش نحصل على الأوكتال ديالي. الرقم لي بقى ناقص هو الرقم الأخير من الجدول لي فيه رقم 1 ولكن أنا ماعندي ماندير بيه اذن غانعوضو برقم 0 وغايولي على هاد الشكل: 110

والنتيجة الأخيرة هي :

(653)₈= (110101011)₂

نشوفو دبا كيفاش نحولو من الهيكزاديسيمال للبينير والعكس:

Hexaecimal to Binary:

(AD15)₁₆

فالقاعدة ديال الهيكزاديسيمال قلنا واحد النقطة لي مهمة ولي هي أن الهيكزا كيكون مكون من عدد فيه أربعة أرقام.. إذن خاصنا نطبقو هاد القاعدة ومانخليوهاش تقولبنا.. غانشدو عاد العدد لي عطاوه لينا فالهيكزا وقالو لينا نحولوه للبينير غانقسموه على ربعة ونحليو كل رقم بوحدو باش يسهال علينا الحساب ومانخربقوهش..

نبداو مع رقم 5 ولي كيساوي لينا فالجدول لي ذكرنا الفوق: 1+4 إذن إلى جيت وعوضت غاندير 11 لكن هنا ماغانكونش حتارمت القاعدة ديال أربعة أرقام, إذن خاصني نعوض بالأصفار.. لكن فين غاندير هاد الأصفار بالضبط؟

غانديرو هاد الجدول باش توضاح الفكرة مزيان.

هنا أنا عوضت 4 و 1 حيت هما لي كيساويو ليا مجموع 5 لي انا باغي.. ودرت 0 فبلاصة 2 وزدت صفر اخر قدامهم باش هاكا نحصل على أربعة الأرقام لي خاصيني باش نكمل العدد ديالي..

كنظن الفكرة وصلات.

ناخذو رقم 1 ونطبقو عليه نفس الشيء